Decimodos's Blog
Just another WordPress.com site
CAPÌTULO 2
- Movimiento
La mecánica trata las relaciones entre fuerza, materia y movimiento; nos disponemos a analizar los métodos matemáticos que describen el movimiento.
Esta parte de la mecánica recibe el nombre de cinemática.
Las siguientes son consideraciones que fundamentan dicho estudio:
- El movimiento puede definirse como un cambio continuo de posición.
- En el movimiento real de un cuerpo extenso, los distintos puntos del mismo se mueven siguiendo trayectorias diferentes, pero consideraremos en principio una descripción del movimiento en función de un punto simple (partícula).
- Tal modelo es adecuado siempre y cuando no exista rotación ni complicaciones similares, o cuando el cuerpo es suficientemente pequeño como para poder ser considerado como un punto respecto al sistema de referencia.
- El movimiento más sencillo que puede describirse es el de un punto en línea recta, la cual haremos coincidir con un eje de coordenadas.
- Desplazamiento, velocidad y aceleración
Para comprender como se mueven los objetos cuando actúan en ellos fuerzas y momentos de rotación externos no equilibrados, es importante configurar exactas imágenes físicas y matemáticas del desplazamiento, la velocidad y la aceleración, comprender las relaciones entre estas tres cantidades.
En el proceso se imaginará un sistema que comprende tres ejes coordenados mutuamente perpendiculares y un pequeño cuerpo en movimiento, que en el curso del tiempo, describe alguna clase de trayectoria en el espacio de coordenadas.
El principio, no se tendrá interés en las fuerzas que provoca este movimiento, ni en la relación entre estas causas físicas y la trayectoria resultante.
En vez de ello, se supondrá que se conoce una ecuación de movimiento que puede resolverse para dar información explícita en todo momento acerca de la posición, la velocidad y la aceleración de la partícula.
Sólo se considerarán los aspectos geométricos del movimiento, cuyo estudio se llama cinemática.
Inicialmente se supone que, de alguna manera, la partícula objeto del estudio está limitada a moverse sólo a lo largo del eje x.
Entonces se puede describir su posición en cualquier instante t por medio de la distancia x entre el origen y la partícula, como hay un valor bien definido de x asociado a cada valor t del tiempo, x es una función de t.
Por lo anterior será posible representar gráficamente el desplazamiento x en función del tiempo y obtener una gráfica como la de la figura (2.1)
Para ver el gráfico seleccione la opción «Descargar» del menú superior
Desplazamiento de un objeto que se mueve sobre el eje x graficado en función del tiempo. La cantidad ∆x/∆t representa la velocidad media en el intervalo de tiempo ∆t, mientras que el límite de esta cantidad cuando ∆t tiende a cero, que es la derivada dx/dt, representa la velocidad instantánea en el tiempo t.
La velocidad media 
durante un intervalo de tiempo 
pude obtenerse determinado la distancia 
que recorre la partícula en ese intervalo, y observando que
(2.2.1)
De la figura 2.1 es claro que es la tangente del ángulo θ, por lo que representa también la pendiente de la secante PQ que une los dos puntos de la curva que corresponde al tiempo t y al desplazamiento x + .
Ahora podrá definirse la velocidad instantánea vx asociada a un instante t y el desplazamiento correspondiente x, como el límite de cuando el intervalo de tiempo tiende a cero. Pero esto es precisamente la definición de la derivada de x con respecto a t; entonces,
(2.2.2)
La velocidad instantánea puede considerarse como la pendiente de la tangente en P a la curva de la figura 2.1.
Es claro que conforme ∆t y ∆x tienden a cero en el límite, la pendiente de la secante PQ se aproxima a la pendiente de la tangente a la curva en P.
Por la ecuación (2.2.2), se puede considerar que la velocidad instantánea Vx es la rapidez de variación del desplazamiento.
Fácilmente se demuestra que si la velocidad instantánea es constante, entonces la velocidad media un intervalo de tiempo es igual a la velocidad instantánea.
Si la velocidad instantánea no fuese constante, entonces la velocidad dependerá del intervalo tiempo escogido y, en general, no será igual a la velocidad instantánea al principio o al final del intervalo.
También se puede hablar de la aceleración media āx durante cierto intervalo, como el cambio en la velocidad instantánea 
que experimenta la partícula durante aquél, dividido entre la duración del mismo,..; entonces,
Como antes, la aceleración instantánea ax asociada al tiempo t se considera como el límite de ax conforme el intervalo tiende a cero, es decir, como la derivada de vx con respecto a t, o bien en vista de (2.1.2), como la segunda derivada de x con respecto a t:
vasquez la mejol
ECUACIONES DE CINEMATICA DE JONATHAN ENCIZO
Todos los cálculos relacionados con las magnitudes que describen los movimientos rectilíneos podemos hacerlos con estas dos ecuaciones:
e es el desplazamiento del móvil Estas ecuaciones se pueden adaptar según las características concretas del movimiento que estemos estudiando: Si el móvil parte del orígen de coordenadas Significa que la posición inicial eo del cuerpo es cero. En este caso la ecuación del desplazamiento podemos escribirla así:
Si el móvil parte del reposo Esto quiere decir que la velocidad inicial es cero. Al sustituir este valor en las ecuaciones anteriores, queda:
Si el movimiento es uniforme Es el movimiento de velocidad constante, es decir el movimiento con aceleración cero. Al dar valor 0 a la aceleración, las ecuaciones del principio quedan así:
Ya habrás notado que no se trata de ecuaciones diferentes sino de las mismas ecuaciones adaptadas a dos casos concretos, por tanto no es necesario que aprendas de memoria todas las ecuaciones: con las dos primeras y un análisis de la situación tienes suficiente. Cómo resolver los ejercicios Para resolver un ejercicio no basta con aplicar las ecuaciones. Es necesario seguir un método o estrategia que podemos resumir así:
Comenzamos haciendo un esquema informativo de la situación física, que aparece un poco más abajo. El segundo paso consiste en identificar los datos que nos proporcionan. Observa que la velocidad final vf es cero porque nos dicen que la moto se detiene. La velocidad inicial vo de la moto es +25 m/s porque esa es la velocidad al inicio del movimiento que estamos estudiando (el movimiento de frenado). La aceleración a es -5 m/s². Presta mucha atención a los signos + y – que tienen las magnitudes. El siguiente paso es saber qué queremos calcular. En nuestro caso, tenemos que determinar el desplazamiento e de la moto mientras frena. A continuación tienes el resultado de los tres primeros pasos:
El cuarto paso consiste en decidir con qué ecuación podemos calcular lo que nos piden y comprobar si tenemos todos los datos que necesitamos. En nuestro caso usaremos la ecuación:
Observa que no podemos calcular e hasta que conozcamos el tiempo t que dura la frenada. Lo podemos calcular con la otra ecuación:
Si sustituimos los valores conocidos de vf, vo y a, tenemos: 0 = 25 m/s + (-5) m/s²·t Una vez calculado el tiempo que dura el movimiento, procedemos a determinar el desplazamiento: e = 25 m/s · 5s + ½ (-5)m/s²·(5s)² e = 62,5 m Hemos llegado a la conclusión de que la moto recorre 62,5 m durante el proceso de frenada. El último paso consiste en comprobar que la solución que damos es correcta y razonable. La solución, en este caso, representa el desplazamiento que realiza la moto desde que se pisa el freno hasta que se detiene. Parece razonable que si se circula a 90 km/h (25 m/s), la distancia necesaria para detener la moto sea aproximadamente las dos terceras partes de un campo de fútbol, similar a la que nosotros hemos obtenido. Para comprobar si los cálculos matemáticos son correctos, sustituye los valores de t y de e que hemos calculado en ambas ecuaciones del movimiento y comprueba que la parte izquierda de cada ecuación sea igual que la derecha. |
ecuaciones de dinamica
Momento angular de una partícula
| Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mvL=r´mv |
Momento angular de un sólido rígido
Las partículas de un sólido rígido en rotación alrededor de un eje fijo describen circunferencias centradas en el eje de rotación con una velocidad que es proporcional al radio de la circunferencia que describen vi=w ·ri
| En la figura, se muestra el vector momento angular Li de una partícula de masa mi cuya posición está dada por el vector ri y que describe una circunferencia de radio Ri con velocidad vi.El módulo del vector momento angular vale Li=rimivi
Su proyección sobre el eje de rotación Z es Liz=miviricos(90-q i), es decir, |
El momento angular de todas las partículas del sólido es
La proyección Lz del vector momento angular a lo largo del eje de rotación es
El término entre paréntesis se denomina momento de inercia
| En general, el vector momento angular L no tiene la dirección del eje de rotación, es decir, el vector momento angular no coincide con su proyección Lz a lo largo del eje de rotación. Cuando coinciden se dice que el eje de rotación es un eje principal de inercia.Para estos ejes existe una relación sencilla entre el momento angular y la velocidad angular, dos vectores que tienen la misma dirección, la del eje de rotación
L=Iw |
El momento de inercia no es una cantidad característica como puede ser la masa o el volumen, sino que su valor depende de la posición del eje de rotación. El momento de inercia es mínimo cuando el eje de rotación pasa por el centro de masa.
| Cuerpo | Momento de inercia Ic |
| Varilla delgada de longitud L | |
| Disco y cilindro de radioR | |
| Esfera de radio R | |
| Aro de radio R | mR2 |
Teorema de Steiner
El teorema de Steiner es una fórmula que nos permite calcular el momento de inercia de un sólido rígido respecto de un eje de rotación que pasa por un punto O, cuando conocemos el momento de inercia respecto a un eje paralelo al anterior y que pasa por el centro de masas.
El momento de inercia del sólido respecto de un eje que pasa por O es
El momento de inercia respecto de un eje que pasa por C es
Para relacionar IO e IC hay que relacionar ri y Ri.
En la figura, tenemos que
El término intermedio en el segundo miembro es cero ya que obtenemos la posición xC del centro de masa desde el centro de masa.
Ejemplo
| Sea una varilla de masa M y longitud L, que tiene dos esferas de masa m y radio r simétricamente dispuestas a una distancia d del eje de rotación que es perpendicular a la varilla y pasa por el punto medio de la misma. |
| Un péndulo consiste en una varilla de masa M y longitud L, y una lenteja de forma cilíndrica de masa m y radio r. El péndulo puede oscilar alrededor de un eje perpendicular a la varilla que pasa por su extremo O |
Energía cinética de rotación
Las partículas del sólido describen circunferencias centradas en el eje de rotación con una velocidad que es proporcional al radio de la circunferencia que describen vi=w ·Ri . La energía cinética total es la suma de las energías cinéticas de cada una de las partículas. Esta suma se puede expresar de forma simple en términos del momento de inercia y la velocidad angular de rotación
Ecuación de la dinámica de rotación
Consideremos un sistema de partículas. Sobre cada partícula actúan las fuerzas exteriores al sistema y las fuerzas de interacción mutua entre las partículas del sistema. Supongamos un sistema formado por dos partículas. Sobre la partícula 1 actúa la fuerza exterior F1 y la fuerza que ejerce la partícula 2, F12. Sobre la partícula 2 actúa la fuerza exterior F2 y la fuerza que ejerce la partícula 1, F21.
Por ejemplo, si el sistema de partículas fuese el formado por la Tierra y la Luna: las fuerzas exteriores serían las que ejerce el Sol ( y el resto de los planetas) sobre la Tierra y sobre la Luna. Las fuerzas interiores serían la atracción mutua entre estos dos cuerpos celestes.
| Para cada unas de las partículas se cumple que la variación del momento angular con el tiempo es igual al momento de la resultante de las fuerzas que actúan sobre la partícula considerada. |
Sumando miembro a miembro, aplicando la propiedad distributiva del producto vectorial, y teniendo en cuanta la tercera Ley de Newton, F12=-F21, tenemos que
Como los vectores r1–r2 y F12 son paralelos su producto vectorial es cero. Por lo que nos queda
La derivada del momento angular total del sistema de partículas con respecto del tiempo es igual al momento de las fuerzas exteriores que actúan sobre las partículas del sistema.
Consideremos ahora que el sistema de partículas es un sólido rígido que está girando alrededor de un eje principal de inercia, entonces el momento angular L=I·w, la ecuación anterior la escribimos
Momento angular de un sistema de partículas
Consideremos el sistema de dos partículas de la figura anterior. El momento angular total del sistema respecto del origen es
L=r1´ m1·v1+r2´ m2·v2
Calculamos el momento angular respecto del centro de masas
r1cm=r1–rcm
r2cm=r2–rcm
v1cm=v1–vcm
v2cm=v2–vcm
El momento angular respecto del origen es la suma de dos contribuciones:
L=(r1cm+rcm) ´ m1·(v1cm+vcm)+ (r2cm+rcm) ´ m2·(v2cm+vcm)=
(r1cm ´ m1·v1cm)+ (r2cm ´ m2·v2cm)+ rcm´ (m1·v1cm+ m2·v2cm)+ (m1·r1cm+ m2·r2cm) ´ vcm
De la definición de posición y velocidad del centro de masas, tenemos que
m1·v1cm+ m2·v2cm=0,
m1·r1cm+ m2·r2cm=(m1+m2)·rcm
L=Lcm+(m1+m2)·rcm ´ vcm
En general, para un sistema de partículas de masa total m
| L=Lcm+m·rcm ´ vcm |
El primer término, es el momento angular interno relativo al sistema c.m. y el último término, el momento angular externo relativo al sistema de laboratorio, como si toda la masa estuviera concentrada en el centro de masa.
Relación entre el momento de las fuerzas exteriores Mext y el momento angular interno Lcm.
El momento de las fuerzas exteriores respecto del origen es la suma de dos contribuciones
Mext= r1´F1+r2´ F2=(r1cm+rcm) ´ F1+(r2cm+rcm) ´ F2= r1cm´ F1+r2cm´ F2+ rcm´ (F1+F2)=
Mcm+ rcm´ (F1+F2).
| Mext= Mcm+ rcm´ Fext. |
El primer término es el momento de las fuerzas exteriores relativo al c.m. y el segundo es el momento de la fuerza resultante F1+F2 como si estuviera aplicada en el centro de masas.
Derivando respecto del tiempo el momento angular total L, tenemos
Teniendo en cuenta que el segundo término es el producto vectorial de dos vectores paralelos y que la ecuación del movimiento del c.m. es
resulta
Como hemos demostrado en el apartado anterior que
Se obtiene la relación
Estas dos relaciones son idénticas pero existen diferencias en su interpretación. En la primera se evalúa el momento angular L y el momento de las fuerzas exteriores Mextrespecto de un punto fijo O (origen del sistema de coordenadas) en un sistema de referencia inercial. La segunda se evalúa el momento angular Lcm y el momento de las fuerzas Mcm respecto al sistema de referencias del centro de masas incluso si no está en reposo con relación al sistema inercial de referencia O.
Esta última relación, es la que emplearemos para describir el movimiento del c.m. de un sólido rígido.
Vamos a estudiar con más detalle la validez de la relación
Siendo A un punto arbitrario, LA el momento angular del sistema de partículas respecto de A y MA el momento total de las fuerzas externas respecto del mismo punto.
| La posición de la partícula i respecto al origen del sistema de referencia inercial es ri, la posición de dicha partícula respecto de A es riA. En la figura, se muestra la relación entre estos dos vectores
ri=rA+riA La velocidad de la partícula i respecto del sistema de referencia inercial es vi, y del punto A es vA. |
El momento angular del sistema de partículas respecto de A, LA es
Sea Fi la fuerza exterior que actúa sobre la partícula i. La segunda ley de Newton afirma que
El momento de las fuerzas exteriores respecto de A es
Como la posición del centro de masas rcm se define
Siendo M la masa total del sistema de partículas, llegamos a la relación
Podemos obtener la misma relación derivando el momento angular LA respecto del tiempo
Cuando el término M(rcm–rA)×aA desaparece, la relación MA=dLA/dt se cumple. Esto ocurre en los siguientes casos:
- Cuando el punto A coincide con el centro de masas rcm=rA
- Cuando la aceleración de A es cero aA =0, es decir, A se mueve con velocidad constante.
- Cuando la aceleración de A, aA es paralela al vector (rcm–rA)
En los ejemplos de la sección Movimiento general de un sólido rígido emplearemos únicamente la relación
El momento angular Lcm del sólido rígido y el momento de las fuerzas exteriores Mcm se calculan con respecto del centro de masas.
Principio de conservación del momento angular
El principio de conservación del momento angular afirma que si el momento de las fuerzas exteriores es cero (lo que no implica que las fuerzas exteriores sean cero, que sea un sistema aislado), el momento angular total se conserva, es decir, permanece constante.
Trabajo y energía en el movimiento de rotación
En otra página relacionamos el trabajo de la resultante de las fuerzas que actúan sobre una partícula con la variación de energía cinética de dicha partícula.
| Considérese un cuerpo rígido que puede girar alrededor de un eje fijo tal como se indica en la figura. Supongamos que se aplica una fuerza exterior F en el punto P. El trabajo realizado por dicha fuerza a medida que el cuerpo gira recorriendo una distancia infinitesimal ds=rdq en el tiempo dt es |
F·senf es la componente tangencial de la fuerza, la componente de la fuerza a lo largo del desplazamiento. La componente radial de la fuerza no realiza trabajo, ya que es perpendicular al desplazamiento.
El momento de la fuerza es el producto de la componente tangencial de la fuerza por el radio. La expresión del trabajo la podemos escribir de forma alternativa
El trabajo total cuando el sólido gira un ángulo q es
En la deducción se ha tenido en cuenta la ecuación de la dinámica de rotación M=Ia , y la definición de velocidad angular y aceleración angular.
Se obtiene una ecuación análoga al teorema trabajo-energía para una partícula. El trabajo de los momentos de las fuerzas que actúan sobre un sólido rígido en rotación alrededor de un eje fijo modifica su energía cinética de rotación.
Impulso angular
En la dinámica de una partícula vimos el concepto de impulso lineal. Una fuerza aplicada durante un tiempo modifica el momento lineal (la velocidad de la partícula).
En el caso de un sólido en rotación la magnitud equivalente se denomina impulso angular.
| El momento de las fuerzas que se aplican durante un tiempo t a un sólido rígido en movimiento de rotación alrededor de un eje fijo, modifica el momento angular del sólido en rotación. |
importancia de la cinematica
importancia de la cinematica
La cinemática estudia los movimientos de los cuerpos independientemente de las causas que lo producen. En este capítulo, estudiaremos los movimientos rectilíneos y curvilíneos, y circulares.
En el caso del movimiento rectilíneo, se simularán dos prácticas que realizan los estudiantes en el laboratorio, que consiste en un móvil que desliza por un carril sin apenas rozamiento. En la primera práctica simulada, se determinará la velocidad constante de un móvil, en la segunda, se determinará la aceleración de un móvil en movimiento uniformemente acelerado.
Ambas prácticas, se prestan especialmente para representar en una gráfica los datos obtenidos y aplicar el procedimiento denominado regresión lineal, trazando la recta que mejor ajusta a los resultados experimentales. Se completa aquí el capítulo primero, en la parte correspondiente a las medidas.
Dos programas interactivos están dedicados a ayudar a los estudiantes a resolver problemas de cinemática. El estudiante puede observar el movimiento de caída de los cuerpos, establecer la posición y la velocidad inicial, y parar el movimiento en cualquier momento. Anotar los valores posición y velocidad del móvil en cualquier instante, y en particular, cuando éste alcanza la altura máxima o regresa al origen. Los valores que el estudiante obtiene resolviendo las ecuaciones del movimiento los puede comparar con los que proporciona el programa interactivo.
La necesidad de establecer un origen y un sistema de referencia para describir un movimiento se pone de manifiesto en la resolución de problemas de caída de los cuerpos. Muchos estudiantes siguen un procedimiento equivocado. Por ejemplo, cuando un cuerpo es lanzado verticalmente hacia arriba calculan la «distancia» recorrida por el cuerpo hasta que alcanza su altura máxima, y luego, la que recorre hasta que llega al suelo, consideran la aceleración negativa como definición del movimiento desacelerado, y les sorprende el signo negativo en la velocidad o en la posición del móvil.
En este capítulo se representan gráficas que describen el movimiento de una partícula. La interpretación de las gráficas es una habilidad que han de conseguir los estudiantes, ya que una gráfica muestra de un vistazo el comportamiento o una tendencia de un fenómeno físico, información que no se puede conseguir mirando una tabla con los mismos datos. La interpretación de las gráficas, posición-tiempo, velocidad-tiempo y aceleración-tiempo, no es tan evidente como pudiera parecer (Beichner 1994).
La principal dificultad de orden didáctico estriba en que los estudiantes no diferencian bien entre el valor de una magnitud y la razón de su cambio con el tiempo. Esta dificultad se pone de manifiesto en las situaciones en las que la velocidad es cero pero la aceleración es distinta de cero, por ejemplo, cuando un móvil que se lanza verticalmente hacia arriba alcanza su altura máxima.
Otros dos programas interactivos, se pueden calificar como problemas-juego, y tratan como otros que se verán a lo largo de este curso, de hacer una Física más intuitiva y divertida. Son programas simples pero significativos desde el punto de vista de la Física. En el primero, se tratará de apuntar con un cañón a un blanco fijo. El estudiante se dará cuenta que hay dos posibles soluciones a este problema. En el segundo, se tratará de bombardear un blanco móvil.
ESTEFANIA VALENCI
problemas de cinemática de manuel valencia
MOVIMIENTO RECTILINEO UNIFORME. 1. Un coche inicia un viaje de 495 Km. a las ocho y media de la mañana con una velocidad media de 90 Km/h ¿A qué hora llegará a su destino? Solución: a las dos de la tarde. 2. Dos trenes se cruzan perpendicularmente y hacen un recorrido durante cuatro horas, siendo la distancia que los separa al cabo de ese tiempo, de 100 km. Si la velocidad de uno de los trenes es de 20 km/h, calcular la velocidad del segundo tren. Solución: v = 15 km/h 3. Dos vehículos cuyas velocidades son 10 Km/h y 12 Km/h respectivamente se cruzan perpendicularmente en su camino. Al cabo de seis horas de recorrido, ¿cuál es la distancia que los separa? Solución: 93,72 km. 4. Dos automóviles que marchan en el mismo sentido, se encuentran a una distancia de 126 Km. Si el más lento va a 42 Km/h, calcular la velocidad del más rápido, sabiendo que le alcanza en seis horas. Solución: v = 63 km/h 5. Un deportista sale de su casa en bici a las seis de la mañana. Al llegar a un cierto lugar, se le estropea la bici y ha de volver andando. Calcular a qué distancia ocurrió el percance sabiendo que las velocidades de desplazamiento han sido de 30 Km/h en bici y 6 Km/h andando y que llegó a su casa a la una del mediodía. Solución: 30 km 6. Un deportista recorre una distancia de 1.000 km, parte en moto y parte en bici. Sabiendo que las velocidades han sido de 120 Km/h en la moto y 20 Km/h en bici, y que el tiempo empleado ha sido de 15 horas calcular los recorridos hechos en moto y en bici. Solución: la motocicleta 840 km y la bici 160 km. 7. Un observador se halla a 510 m. de una pared. Desde igual distancia del observador y de la pared, se hace un disparo ¿al cabo de cuántos segundos percibirá el observador : a) el sonido directo. b) el eco? Velocidad del sonido 340 m/s. Solución: el sonido directo a 0,75 s, y el del eco a 2,25 s. 8. Un ladrón roba una bicicleta y huye con ella a 20 km/h. Un ciclista que lo ve, sale detrás del mismo tres minutos más tarde a 22 Km/h. ¿Al cabo de cuánto tiempo lo alcanzará? Solución: 30 minutos. 9. Calcular la longitud de un tren cuya velocidad es de 72 Km/h y que ha pasado por un puente de 720 m de largo, si desde que penetró la máquina hasta que salió el último vagón han pasado ¾ de minuto. Solución: 180 metros. 10. Dos coches salen a su encuentro, uno de Bilbao y otro de Madrid. Sabiendo que la distancia entre ambas capitales es de 443 Km. y que sus velocidades respectivas son 78 Km/h y 62 Km/h y que el coche de Bilbao salió hora y media más tarde, calcular : a) Tiempo que tardan en encontrarse b) ¿A qué distancia de Bilbao lo hacen? Solución: tardan en encontrarse 2,5 horas; a 195 km de Bilbao.
Programación por niveles: Estática y dinámica. Actividades para el nivel superior. Alumnos avanzados
Pretenden ser actividades para el desarrollo de las destrezas en el aprendizaje de la física, para aprender jugando, si practicas con ellas, y te sirve de entretenimiento, creo que merece la pena el esfuerzo de prepararlas… ¡Ánimo y a jugar!
Mecánica:
Inicio al estudio de los movimientos. Visualización del desplazamiento de un coche, con contadores de posición, velocidad y aceleración. Se pueden visualizar vectores aceleración y velocidad… y realizar cálculos diversos. Practicar…
Test de elección múltiple, para que aprendas y solidifiques tus conocimientos sobre CINEMÁTICA. En el tienes 30 preguntas, para simplificar la carga de la página, cada vez que actualices la página de los test se cargarán sólamente 10 preguntas. Cuando superes el test, puedes cargar otro… hasta que te canses.
Actividades Para trabajar con las representaciones gráficas y los cálculos sobre gráficas, aquí tienes dos programillas, que se autoejecutan desde este mismo sitio, o bien puedes abrirlos en una nueva ventana, para hacer prácticas:
Distancia/ tiempo: Con este juego, al pulsar sobre el botón de nuevo ejemplo, obtienes una gráfica en la que tienes que calcular (con lápiz y papel…):
a) la velocidad en cada tramo;
b) distancia y tiempo al origen;
c) distancia total recorrida.Tras los cálculos realizados, puedes comprobar lo fino que has estado… ¡Que lo disfrutes!
Velocidad/tiempo : Similar al juego anterior, pero para el estudio del movimiento uniforme acelerado. ¡Juega con ellos!
PROBLEMAS DE DINAMICA
Una bala de 5 gramos lleva una velocidad de 400 m /s , choca y se empotra contra un bloque de madera de 5 Kg, suspendido formando un péndulo. Determinar la altura a que se elevará el bloque después del impacto y la fuerza resistente de la madera a la penetración si la bala penetró 12 cm.
Por ser un choque inelástico se cumple el teorema de conservación de la cantidad de movimiento, pero no se cumple el de conservación de la energía. Sea v1 la velocidad del bloque con la bala justo después del impacto:
S (mi.vi)]antes = S (mi.vi)]después ® m. v = (m + M). v1
® v1 = v. m /(m + M) = 400. 0’005 / (0’005 + 5) = 0’4 m /s
A partir de este momento, debido al impulso recibido, el bloque con la bala se eleva, conservando su energía, por lo que la energía en el punto más alto es igual a la energía de salida:
Esalida = Epunto más alto ® ½. (m + M). v12 = (m + M).g. h
® h = ½. v12 /g = [ v. m /(m + M)]2 /(2g) = [ 400. 0’005 /(0’005 + 5)]2 /(2.9’8) = 0’0081 m
Durante el choque, la pérdida de energía se invierte en penetrar la bala en el bloque:
Eantes del choque – Edespués del choque = W ® ½. m. v2 – ½. (m + M). v12 = W = F. e
® F = [½. m. v2 – ½. (m + M). v12 ] / e = [½. m. v2 – ½. (m + M). [v. m /(m + M)]2 ] / e
F = ½. m. v2 . [ 1 – m /(m + M) ] / e = ½. m. v2 / [e.(m + M) ]
F = ½. 0’005. 4002 / [0’12.(0’005 + 5) ] = 660 N
La fuerza por unidad de longitud será: F/L = 660 / 0’12 = 5500 N /m.
Un cuerpo de 60 Kg está en reposo sobre un plano inclinado 60º y está unido mediante una cuerda sin masa a otro cuerpo de 70 kg que está en un plano inclinado 30º. Si el coeficiente de rozamiento en ambos planos es 0’1, determinar la aceleración del sistema.
En cada cuerpo las fuerzas existentes son:
el peso, P
la reacción del plano, R
la fuerza de rozamiento, Fr
La reacción del plano, R , es igual a la componente normal del peso, N :
R1 = N1 = P1. cos a = 60. 9’8. cos 60 = 294 N
R2 = N2 = P2. cos b = 70. 9’8. cos 30 = 594 ‘ 1 N
El sentido del movimiento, si se mueve, vendrá dado por la mayor de las componentes tangenciales de los pesos, en este caso hacia la izquierda:
T1 = P1. sen a = 60. 9’8. sen 60 = 509 ‘ 2 N
T2 = P2.sen b = 70. 9’8. sen 30 = 343 N
Las fuerzas de rozamiento son:
Fr1 = m . N1 = 0’1. 294 = 29 ‘ 4 N
Fr2 = m . N2 = 0’1. 594’1 = 59 ‘ 41 N
La fuerza total que actúa sobre el sistema será:
F = T1 – ( T2 + Fr1 + Fr2 ) = 509’2 – ( 343 + 29’4 + 59’41 ) = 77 ‘ 39 N
La aceleración del movimiento será:
a = F / M = 77’39 / (60 + 70) = 0 ‘ 595 m /s2.
Un objeto de 4 kg de mas, inicialmente en reposo, estalla en tres fragmentos de masas 2 kg, 1 kg, y 1 kg. El bloque de 2 kg sale con velocidad de 600 m/s y los otros formando 30º y -45º con relación al primero. Determinar sus velocidades.
Al no existir ninguna fuerza exterior, la cantidad de movimiento debe permanecer constante e igual a cero pues antes de estallar el sistema está en reposo.
Según el eje X:
m1.v1. cos 30 + m2.v2. cos 45 – mo.vo = 0
v1. cos 30 + v2. cos 45 =2.600= 1200
Según el eje Y:
m1.v1. sen 30 + m2.v2. sen 45 – mo.0 = 0
v1. sen 30 + .v2. sen 45 = 0
Resolviendo el sistema se obtiene:
v1 = 878 m /s v2 = 621 m /s.
Las aspas de un molino son uniformes de masa 200 kg y de longitud 7 m. Sus extremos giran a una velocidad máxima de 36 Km /h. Determinar la fuerza que deben soportar los pernos de unión al eje.
La fuerza que soportan los pernos que sujetan el aspa al eje será la fuerza centrípeta que la obliga a girar más la acción del peso.
Sea r la densidad lineal del ala: r = m /L
Consideremos la fuerza centrípeta sobre un diferencial de masa e integremos para todo el ala:
La fuerza máxima será cuando el aspa esté en la vertical inferior: F = Fc + m.g.
CAPÌTULO 2
- Movimiento
La mecánica trata las relaciones entre fuerza, materia y movimiento; nos disponemos a analizar los métodos matemáticos que describen el movimiento.
Esta parte de la mecánica recibe el nombre de cinemática.
Las siguientes son consideraciones que fundamentan dicho estudio:
- El movimiento puede definirse como un cambio continuo de posición.
- En el movimiento real de un cuerpo extenso, los distintos puntos del mismo se mueven siguiendo trayectorias diferentes, pero consideraremos en principio una descripción del movimiento en función de un punto simple (partícula).
- Tal modelo es adecuado siempre y cuando no exista rotación ni complicaciones similares, o cuando el cuerpo es suficientemente pequeño como para poder ser considerado como un punto respecto al sistema de referencia.
- El movimiento más sencillo que puede describirse es el de un punto en línea recta, la cual haremos coincidir con un eje de coordenadas.
- Desplazamiento, velocidad y aceleración
Para comprender como se mueven los objetos cuando actúan en ellos fuerzas y momentos de rotación externos no equilibrados, es importante configurar exactas imágenes físicas y matemáticas del desplazamiento, la velocidad y la aceleración, comprender las relaciones entre estas tres cantidades.
En el proceso se imaginará un sistema que comprende tres ejes coordenados mutuamente perpendiculares y un pequeño cuerpo en movimiento, que en el curso del tiempo, describe alguna clase de trayectoria en el espacio de coordenadas.
El principio, no se tendrá interés en las fuerzas que provoca este movimiento, ni en la relación entre estas causas físicas y la trayectoria resultante.
En vez de ello, se supondrá que se conoce una ecuación de movimiento que puede resolverse para dar información explícita en todo momento acerca de la posición, la velocidad y la aceleración de la partícula.
Sólo se considerarán los aspectos geométricos del movimiento, cuyo estudio se llama cinemática.
Inicialmente se supone que, de alguna manera, la partícula objeto del estudio está limitada a moverse sólo a lo largo del eje x.
Entonces se puede describir su posición en cualquier instante t por medio de la distancia x entre el origen y la partícula, como hay un valor bien definido de x asociado a cada valor t del tiempo, x es una función de t.
Por lo anterior será posible representar gráficamente el desplazamiento x en función del tiempo y obtener una gráfica como la de la figura (2.1)
Para ver el gráfico seleccione la opción «Descargar» del menú superior
Desplazamiento de un objeto que se mueve sobre el eje x graficado en función del tiempo. La cantidad ∆x/∆t representa la velocidad media en el intervalo de tiempo ∆t, mientras que el límite de esta cantidad cuando ∆t tiende a cero, que es la derivada dx/dt, representa la velocidad instantánea en el tiempo t.
La velocidad media durante un intervalo de tiempo pude obtenerse determinado la distancia que recorre la partícula en ese intervalo, y observando que
(2.2.1)
De la figura 2.1 es claro que es la tangente del ángulo θ, por lo que representa también la pendiente de la secante PQ que une los dos puntos de la curva que corresponde al tiempo t y al desplazamiento x + .
Ahora podrá definirse la velocidad instantánea vx asociada a un instante t y el desplazamiento correspondiente x, como el límite de cuando el intervalo de tiempo tiende a cero. Pero esto es precisamente la definición de la derivada de x con respecto a t; entonces,
(2.2.2)
La velocidad instantánea puede considerarse como la pendiente de la tangente en P a la curva de la figura 2.1.
Es claro que conforme ∆t y ∆x tienden a cero en el límite, la pendiente de la secante PQ se aproxima a la pendiente de la tangente a la curva en P.
Por la ecuación (2.2.2), se puede considerar que la velocidad instantánea Vx es la rapidez de variación del desplazamiento.
Fácilmente se demuestra que si la velocidad instantánea es constante, entonces la velocidad media un intervalo de tiempo es igual a la velocidad instantánea.
Si la velocidad instantánea no fuese constante, entonces la velocidad dependerá del intervalo tiempo escogido y, en general, no será igual a la velocidad instantánea al principio o al final del intervalo.
También se puede hablar de la aceleración media āx durante cierto intervalo, como el cambio en la velocidad instantánea que experimenta la partícula durante aquél, dividido entre la duración del mismo,..; entonces,
Como antes, la aceleración instantánea ax asociada al tiempo t se considera como el límite de ax conforme el intervalo tiende a cero, es decir, como la derivada de vx con respecto a t, o bien en vista de (2.1.2), como la segunda derivada de x con respecto a t:
vasquez la mejol
teoria cinematica «claminton»
El fenómeno más obvio y fundamental que observamos a nuestro alrededor es el de movimiento. El viento, las olas, los pájaros que vuelan, los animales que corren, las hojas que caen. Prácticamente todos los procesos inimaginables pueden describirse como el movimiento de ciertos objetos. Para analizar y predecir la naturalezade los movimientos que resultan de las diferentes clases de interacciones, se han inventado algunos conceptos importantes tales como los de momentum, fuerzay energía. Si el momentum, la fuerza, y la energía se conocen y se expresan en un modo cuantitativo es posible establecer reglas mediante las cuales pueden predecirse los movimientos resultantes.
La mecánica, es la ciencia del movimiento, es también la ciencia del momentum, la fuerza y la energía; de ella se derivan: la cinemática, que estudia el movimiento sin tomar en consideración las fuerzas que lo producen, y la dinámica, que a diferencia de la cinemática, fundamenta el estudio del movimiento en las leyes del movimiento propuestas por Newton.
En este material instruccional se introducirá en forma sucinta los movimientos clásicos que se asocian a la cinemática: movimiento rectilíneo acelerado y no acelerado, movimiento curvilíneo, movimiento parabólico y caída libre. Se presentará los conceptos de aceleración tangencial, aceleración radial y radio de curvatura; todos ellos de manifiesto en los movimientos circulares. Un apartado será dedicado a la cinemática vectorial; aquí, el álgebra con vectores se empleará en la caracterización de los movimientos. Se expondrá las leyes del movimiento de Newton, y la manera como éstas se aplican al análisisde una amplia variedad de movimientos. En determinadas situaciones se incluirá en el análisis, fuerzas de rozamiento, en sus dos variantes: fuerzas de rozamiento estático y fuerza de rozamiento dinámico. Al final, se ofrecerá una recopilación de algunos problemas que han formado parte de las evaluaciones de cohortes precedentes.
Al término de éste módulo, el estudiante tendrá la habilidad y pericia necesaria para aplicar los conceptos básicos de cinemática y dinámica en la resolución de problemas prácticos que involucren movimientos tanto en el plano como en el espacio.
- Movimiento uniforme acelerado y no acelerado.
- Características cinemáticas de cuerpos en caída libre.
- Características cinemáticas de cuerpos en movimiento parabólico.
- Características cinemáticas de cuerpos en movimiento circular.
- Leyes del movimiento de Newton.
- Fuerzas de rozamiento: estático y dinámico.
- Cinemática vectorial: vector posición, vector velocidad y vector aceleración.
- Cinemática vectorial: radio de curvatura en movimientos circulares.
CONOCIMIENTOS PREVIOS
- Multiplicación de vectores: escalar y vectorial.
- Álgebra matricial: matriz adjunta y teorema del cofactor.
- Cálculo infinitesimal: límite y derivación de funciones matemáticas.
- Cálculo integral: integrales definidas con límites de integración.
- Trigonometría plana.
- Descomposición rectangular de vectores: Diagrama de Cuerpo Libre (DCL).
1.1 Diferencia entre cinemática y dinámica.
La cinemática, es un área de estudio de la mecánica que describe el movimiento en función del espacio y el tiempo, sin tomar en cuenta los agentes presentes que lo producen. Por su parte, la dinámica es un área de estudio de la mecánica que describe el movimiento en cuanto al espacio y el tiempo, considerando los agentes presentes que lo producen.
En cinemática es de gran importancia definir un referencial, el cual es un marco de referencia, cuya característica principal es la de no estar acelerado. Cualquier marco de referencia que se mueve con velocidad constante respecto de un marco inercial es por sí mismo un marco inercial.
1.2 Velocidad y aceleración: ecuaciones básicas.
La velocidad media de una partícula durante un intervalo de tiempo t, está definida como la razón entre el desplazamiento y el intervalo de tiempo (Figura 1).
(1)
Donde:
: Velocidad media del móvil, m/s
: Magnitud del desplazamiento del móvil, m
Intervalo de tiempo, s
Como el desplazamiento es una cantidad vectorial y el intervalo de tiempo es una cantidad escalar, concluimos que la velocidad promedio es una cantidad vectorial dirigida a lo largo de .
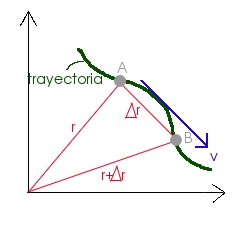
Figura 1. Una partícula que se mueve en el plano x-y se localiza a través del vector posición 
dibujado desde el origen del sistema referencial inercial. El desplazamiento de la partícula cuando se mueve de P a Q en el intervalo 
= tf – ti, es igual al vector = 
.
Un concepto derivado de la velocidad media, es la velocidad instantánea, la cual se define como el límite de la velocidad promedio, 
, conforme tiende a cero.
(2)
La velocidad instantánea es igual a la derivada del vector de posición respecto del tiempo. La dirección del vector velocidad instantánea en cualquier punto en una trayectoria de la partícula está a lo largo de la línea que es tangente a la trayectoria en ese punto y en la dirección del movimiento. A la magnitud del vector de velocidad instantánea recibe el nombre de «rapidez».
La velocidad media al igual que la velocidad instantánea se expresa m/s en el sistema internacional; Ft/s en el sistema británico (se lee pies por segundo), y cm/s en el sistema c.g.s.
Dado que la velocidad de un móvil puede variar en el tiempo, nació un concepto denominado aceleración, la cual se define como la razón de cambio del vector velocidad, 
, en un tiempo transcurrido .
(3)
Donde:
Vf: velocidad final del movimiento, m/s
Vi: velocidad inicial del movimiento, m/s
tf – ti: intervalo de tiempo trascurrido para que el móvil pase de Vi a Vf.
Puesto que la aceleración promedio es la razón entre una cantidad vectorial, , y una cantidad escalar, , se concluye que, 
, es una cantidad vectorial dirigida a lo largo de .
Un concepto derivado de la aceleración promedio, es la aceleración instantánea, la cual se define como el valor límite de la razón , cuando, , tiende a cero.
(4)
En otras palabras, la aceleración instantánea es igual a la razón de cambio del vector velocidad respecto al tiempo.
Es importante tener en cuenta tres situaciones donde un móvil tiene una aceleración asociada: cuando la magnitud del vector (la rapidez) cambia con el tiempo; como en un movimiento acelerado en línea recta; cuando sólo la dirección del vector velocidad cambia con el tiempo sin que su magnitud varíe, como en un movimiento curvilíneo; y por último, cuando tanto la magnitud como la dirección del vector velocidad se modifican continuamente.
La aceleración media, así como la aceleración instantánea se expresan en m/s2 en el sistema internacional, en Ft/s2 en el sistema británico (se lee pies por segundo cuadrado), y cm/s2 en el sistema c.g.s.
El hecho de que un cuerpo se desplace con una aceleración de 15 m/s2, implica que cada segundo su velocidad aumenta 15 m/s. También pudiese darse el caso de que un móvil ostente una aceleración negativa, por ejemplo de – 8 m/s2, lo cual indica que cada segundo su velocidad decae 8 m/s. Por último, si un móvil tiene una aceleración igual a cero, puede inferirse que: posee una velocidad constante, o se encuentra en reposo.
1.3 Movimiento rectilíneo uniforme.
Haciendo uso del cálculo integral, se deducirán las ecuaciones cinemáticas que gobiernan el movimiento unidimensional (significa que se da a lo largo de una línea recta).
Como la aceleración de un móvil está dada por: 
despejando dv, queda…
dv = a.dt la cual por integración, resulta…
(5)
Asumiendo que la aceleración es constante a lo largo del tiempo (movimiento con aceleración constante), nos queda:
v = a.t + C1 (6)
Donde:
a: aceleración del móvil, m/s2
t: tiempo, s
C1: constante de integración,m/s
El valor C1 depende de las condiciones iniciales del movimiento. Si se toma v = v0 cuando t = t0 y sustituimos estos valores en la ecuación 6, se tendrá…
v = a [0] + C1 despejando C1…
C1 = v0 (7)
Por tanto, se obtiene la primera ecuación cinemática (Ecuación 8), la cual relaciona la velocidad del móvil con su aceleración.
v = vo + a.t (8)
Ahora considerando la ecuación que define la velocidad instantánea: 
y despejando dx, nos queda:
dx = v.dt (9)
Integrando la Ecuación 9, resulta…
(10)
No obstante, dado que según la Ecuación 8: v = v0 + a.t, nos queda…
integrando…
(11)
Donde:
x: distancia recorrida, m
vo: velocidad inicial del móvil, m/s
t: tiempo, s
a: aceleración del móvil, m/s2
C2: constante de integración, m
Para encontrar C2, se toma en cuenta la siguiente condición inicial x = x0, cuando t = 0. Esto produce C2 = x0. En consecuencia, se obtiene:
(12)
La Ecuación 12 relaciona: la velocidad inicial, el tiempo y la aceleración del móvil con la distancia por él recorrida.
Figura 2. Gráfica velocidad – tiempo. Una partícula que se mueve a lo largo del eje x con aceleración constante, a. La aceleración matemáticamente equivale a la pendiente de la gráfica superior, el punto de corte con el eje de velocidades, es la velocidad inicial del móvil.
La Figura 2, revela que la aceleración puede calcularse aplicando la definición de pendiente, o sea:
(13)
Cuando el movimiento es unidimensional, la velocidad promedio en cualquier intervalo de tiempo es calculada como la media aritmética de la velocidad inicial, v0, y la velocidad final, v.
(14)
Donde:
: velocidad media del móvil, m/s
vo: velocidad inicial del móvil, m/s
v: velocidad inicial del móvil en cualquier tiempo t, m/s
Según la Ecuación 8, v = v0 + a.t; despejamos t…
(15)
Dado que la Ecuación 12 establece que:; se introduce la Ecuación 15 en la Ecuación 12…
desarrollando, queda…
(16)
Donde:
v: velocidad final del móvil, m/s
vo: velocidad inicial del móvil, m/s
a: aceleración del móvil, m/s2
x – xo: distancia que recorre el móvil al pasar de vo a vf, m
Esta última fórmula establece la velocidad como una función del desplazamiento.
1.4 Lanzamiento horizontal: ecuaciones asociadas.
En éste tipo de lanzamiento el cuerpo está sometido simultáneamente a la acción de dos movimientos:
- Uno horizontal, con velocidad constante.
- Otro vertical, el cual es uniformemente acelerado.
Estos dos movimientos hacen que el desplazamiento resultante sea de una trayectoria parabólica, además, ambos son completamente independiente uno del otro, tal como lo demostró Galileo, mediante experimentos que lo llevaron a enunciar su «Principio de la independencia de los movimientos».
- Uno horizontal, con velocidad constante.
- Otro vertical, el cual es uniformemente acelerado.
Estos dos movimientos hacen que el desplazamiento resultante sea de una trayectoria parabólica, además, ambos son completamente independiente uno del otro, tal como lo demostró Galileo, mediante experimentos que lo llevaron a enunciar su «Principio de la independencia de los movimientos».
Figura 3. En este caso el disparo se hace desde una altura «Y» como lo indica la figura con una velocidad inicial 
, al iniciar su caída estará sometido el proyectil a la acción de dos movimientos: uno horizontal con velocidad constante y otro vertical uniformemente acelerado hacia abajo debido a la fuerza de gravedad.
En este movimiento, la componente horizontal de la velocidad es de magnitud constante a través de todo el recorrido e igual a, .
= (17)
La componente vertical de la velocidad, 
, en un instante de tiempo cualquiera viene dada por:
= 
.t (18)
Donde:
vy: velocidad vertical del móvil, m/s
: constante de gravedad = 9,81 m/s2.
t: tiempo recorrido, s
Aplicando el Teorema de Pitágoras, es posible determinar el módulo del vector velocidad en cualquier instante, pues las componentes de la velocidad son ortogonales entre si, en todo momento.
(19)
Donde:
vx: componente horizontal de la velocidad del móvil, m/s
vy: componente vertical de la velocidad del móvil, m/s
La dirección del vector velocidad queda definida por la función tangente del ángulo .
(20)
La ecuación de posición horizontal es la misma del movimiento rectilíneo no acelerado, puesto que la rapidez en este sentido es constante, escribiéndose como:
x = v0.t (21)
La posición vertical se calcula como si el cuerpo se moviese en caída libre;
(22)
Donde:
y: distancia vertical que el móvil se ha desplazado, m
: constante de gravedad = 9,81 m/s2.
t: tiempo recorrido, s
El signo negativo en la Ecuación 22, se debe al vector gravedad, el cual esta dirigido verticalmente hacia el centro de la Tierra.
El desplazamiento total se obtiene aplicando el Teorema de Pitágoras, pues el desplazamiento vertical y horizontal son ortogonales entre si.
(23)
Donde:
x: componente horizontal del desplazamiento, m
y: componente vertical del desplazamiento, m
La dirección del desplazamiento se obtiene aplicando la definición de tangente.
(24)
Un término ampliamente usado en movimientos que se dan bajo un campo gravitatorio, es el tiempo de vuelo, el cual es el tiempo transcurrido desde el momento del lanzamiento hasta tocar el suelo. Al tocar el suelo el móvil ha recorrido todo la distancia vertical «Y» (Figura 3), pudiéndose escribir de acuerdo a la Ecuación 22:
despejando tv…
(25)
El alcance horizontal, es el desplazamiento total horizontal que el móvil posee al cumplirse el tiempo de vuelo. La ecuación para calcular el alcance horizontal es la misma del desplazamiento horizontal, pero con t = tv
R = v0. tv(26)
A continuación se demuestra que la trayectoria del proyectil es parabólica. En efecto, el desplazamiento horizontal para cierto tiempo «t» viene dado por:
x = v0 . t despejando » t » nos queda…
(27)
Por otra parte el desplazamiento vertical al mismo tiempo «t» esta dada por la Ecuación 22…
; como el tiempo para ambos desplazamientos es el mismo, podemos sustituir «t» de la Ecuación 27 en «t» de la Ecuación 22, quedando…
(28)
Como v0 (velocidad inicial) y g (aceleración de gravedad) son constantes se tendrá que:
y = k.x2 (29)
En donde 
(término constante)
Como puede notarse, la Ecuación 29 corresponde a la ecuación de una parábola, con lo que se concluye que la trayectoria del movimiento es esencialmente parabólica.
1.5 Lanzamiento inclinado: ecuaciones asociadas.
Al igual que el lanzamiento horizontal, el proyectil estará sometido a la acción de dos movimientos (Figura 4):
- Uno horizontal con velocidad constante, es decir, la componente horizontal de la aceleración es cero.
- Otro vertical con aceleración constante, dirigida hacia abajo.
Figura 4. Al lanzarse un proyectil inclinados un ángulo , con una velocidad inicial «vo», se produce un movimiento en el cual se superponen dos movimientos independientes: uno horizontal no acelerado, y otro influido por la fuerza de gravedad, precisamente éste último ocasiona que la trayectoria seguida por el móvil sea parabólica.
Cuando el proyectil ocupa la posición P de la Figura 4, un instante «t» después de haber sido lanzado, la velocidad, 
, tendrá una componente horizontal,
, y otra vertical,
. La magnitud de la componente horizontal de la velocidad se mantiene constante a través de todo el recorrido y está dada por:
(30)
Donde:
vx: componente horizontal de la velocidad, m/s
vox: componente horizontal de la velocidad inicial, m/s
: ángulo de disparo, grados
La magnitud de la componente vertical de la velocidad en cualquier instante está dada por:
(31)
Donde:
vy: componente vertical de la velocidad, m/s
vox: componente vertical de la velocidad inicial, m/s
g: aceleración de gravedad = 9,81 m/s2
t: tiempo, s
Dado que las componentes de la velocidad son ortogonales entre si, la magnitud de la velocidad en cualquier instante viene dada por:
(32)
El ángulo que el vector velocidad total forma con el eje horizontal permite definir la dirección del referido vector:
(33)
El movimiento horizontal lo realiza el proyectil con velocidad constante, por lo que el desplazamiento horizontal (x) viene dado por:
(34)
El movimiento vertical lo realiza con aceleración constante, 
, dirigida hacia abajo, por lo que la ecuación de desplazamiento vertical, queda definida por:
(35)
El tiempo empleado por el proyectil en alcanzar la altura máxima [ymáx], es denominado tiempo máximo. Observando la Figura 4, puede notarse que, a medida que el proyectil asciende va disminuyendo su velocidad a lo largo del eje y [
] hasta hacerse cero en el vértice de la parábola descrita.
Según la Ecuación 31 y sabiendo que la velocidad vertical en el punto de máxima altura es cero.
despejando tmáx…
(36)
Por otra parte, la altura máxima la obtenemos haciendo t = tmáx en la Ecuación 35, quedandonos…
ahora, sustituimos de acuerdo a la Ecuación 36…
Nos queda 
desarrollando…
(37)
Donde:
ymáx: máxima altura que alcanza el proyectil, m
vox: componente vertical de la velocidad inicial, m/s
g: aceleración de gravedad = 9,81 m/s2
El tiempo de vuelo es el tiempo que trascurre para que el proyectil vaya desde A hasta B (refiérase a la Figura 4).
(38)
Las fórmulas desarrolladas tanto para el lanzamiento horizontal como vertical, no consideran el efecto resistivo del aire, la curvatura de la superficie terrestre, ni la variación gravitacional.
1.6 Movimiento circular: ecuaciones asociadas.
Ante de iniciar este apartado, se debe hablar del desplazamiento angular; el cual se refiere a los grados, vueltas, revoluciones ó radianes que el cuerpo se desplaza a lo largo de la trayectoria circunferencial. Una revolución es equivalente a 360º ó 2 radianes.
Cuando se habla de la velocidad angular de un cuerpo, se refiere a la variación del desplazamiento angular que experimenta por unidad de tiempo. Se expresa en radianes/s o bien, grados/s, revolución/s, o revolución/min [conocida como RPM]. Si un cuerpo se desplaza un ángulo «» radianes en un tiempo de «t» segundos, su velocidad angular media 
[rad/s] se define por la relación:
Information
Change this sentence and title from admin Theme option page.
Recent entry
- 2010-09-13
- claudia mosquera ecuasiones
- 2010-09-13
- lady chicangana
- 2010-08-30
- 2010-08-30
- ECUACIONES DE CINEMATICA DE JONATHAN ENCIZO
- 2010-08-30
- ECUACIONES DE CINEMATICA DE JONATHAN ENCIZO
Decimodos's Blog 